9. Line Integrals
The arc length integral can be generalized to the integral of any function.
b. Line Integrals of Scalars
The line integral of a function, \(f(x,y,z)\), along a parametric curve, \(\vec r(t)=\left(x(t),y(t),z(t)\right)\), between \(A=\vec r(a)\) and \(B=\vec r(b)\) is given by \[ \int_A^B f\,ds =\int_a^b f(\vec r(t))|\vec v|\,dt \] where \(f(\vec r(t))\) is the composition of \(f\) and \(\vec r\), i.e. the function \(f(x,y,z)\) with \(x\), \(y\) and \(z\) replaced by \(x(t)\), \(y(t)\) and \(z(t)\). The composition \(f(\vec r(t))\) is called the value of the function along the curve or the restriction of the function to the curve.
We sometimes write \(f(t)\) to mean \(f(\vec r(t))\), the value of \(f\) at time \(t\), even though this is not mathematically correct. Consequently, this is sometimes called abuse of notation.
Notice that we again switch the limits on the integral from the abstract points \(A\) and \(B\) to the values \(a\) and \(b\) of the parameter \(t\) when we switch from the integral with the general differential \(ds\) to the integral with the parameter differential \(dt\).
Compute \(\displaystyle \int_{(0,0,0)}^{(1,1,2/3)} (3xz+y^2)\,ds\) along the twisted cubic \(\vec r(t)=\left(t,t^2,\dfrac{2}{3}t^3\right)\).
The value of the function along the curve is \[ f(\vec r(t)) =3x(t)z(t)+y(t)^2 =3(t)\left(\dfrac{2}{3}t^3\right)+(t^2)^2=3t^4 \] The velocity is \(\vec v=(1,2t,2t^2)\) and its length is \(|\vec v|=\sqrt{1+4t^2+4t^4}=\sqrt{(1+2t^2)^2}=1+2t^2\). Finally, the endpoints are: \[ (0,0,0)=\vec r(0) \qquad \left(1,1,\dfrac{2}{3}\right)=\vec r(1) \] So \[\begin{aligned} \int_{(0,0,0)}^{(1,1,2/3)} (3xz+y^2)\,ds &=\int_0^1 f(\vec r(t))|\vec v|\,dt =\int_0^1 3t^4(1+2t^2)\,dt \\ &=\left[\dfrac{3}{5}t^5+\dfrac{6}{7}t^7\right]_0^1 =\dfrac{3}{5}+\dfrac{6}{7}=\dfrac{51}{35} \end{aligned}\]
Compute \(\displaystyle \int x^2\,ds\) along the helix
\(x=4\cos\dfrac{z}{3},\quad y=4\sin\dfrac{z}{3}\)
between \(z=0\) and \(z=6\pi\). You can rotate this plot with your mouse.

For functions of \(z\), the differential of arc length is \[ ds=\sqrt{\left(\dfrac{dx}{dz}\right)^2+\left(\dfrac{dy}{dz}\right)^2+1}\,dz \]
\(\displaystyle \int x^2\,ds=80\pi\)
The derivatives are: \[ \dfrac{dx}{dz}=-\,\dfrac{4}{3}\sin\dfrac{z}{3} \qquad \text{and} \qquad \dfrac{dy}{dz}=\dfrac{4}{3}\cos\dfrac{z}{3} \] So the differential of arc length is \[\begin{aligned} ds&=\sqrt{\left(\dfrac{dx}{dz}\right)^2+\left(\dfrac{dy}{dz}\right)^2+1}\,dz \\ &=\sqrt{\left(-\,\dfrac{4}{3}\sin\dfrac{z}{3}\right)^2 +\left(\dfrac{4}{3}\cos\dfrac{z}{3}\right)^2+1}\,dz \\ &=\sqrt{\dfrac{16}{9}+1}\,dz=\dfrac{5}{3}\,dz \end{aligned}\] Thus, using the identity \(\cos^2A=\dfrac{1+\cos2A}{2}\): \[\begin{aligned} \int x^2\,ds &=\int_0^{6\pi} 16\cos^2\left(\dfrac{z}{3}\right)\dfrac{5}{3}\,dz =\dfrac{80}{3}\int_0^{6\pi} \dfrac{1+\cos\dfrac{2z}{3}}{2}\,dz \\ &=\dfrac{40}{3}\left[z+\dfrac{3}{2}\sin\dfrac{2z}{3}\right]_0^{6\pi} =80\pi \end{aligned}\]
Compute \(\displaystyle \int_{(4,0,0)}^{(4,0,6\pi)} (x^2+y^2+z^2)\,ds\) along the helix \(\vec r(t)=(4\cos t,4\sin t,3t)\).
Notice this is the same helix as in the previous exercise, except written in parametric form.
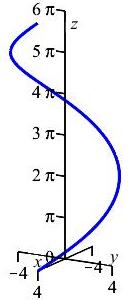
\(\displaystyle \int_{(4,0,0)}^{(4,0,6\pi)} (x^2+y^2+z^2)\,ds =160\pi+120\pi^3\)
We first identify the integrand and evaluate it on the curve: \[\begin{aligned} f&=x^2+y^2+z^2 \\ f(\vec r(t))&=16\cos^2t+16\sin^2t+9t^2=16+9t^2 \end{aligned}\] The velocity is \(\vec v(t)=(-4\sin t,4\cos t,3)\) and its length is \(|\vec v|=5\). Also, the point \((4,0,0)\) occurs at \(t=0\) and the point \((4,0,6\pi)\) occurs at \(t=2\pi\). So the integral becomes: \[\begin{aligned} \int_{(4,0,0)}^{(4,0,6\pi)} &(x^2+y^2+z^2)\,ds =\int_0^{2\pi} (16+9t^2)5\,dt \\ &=5\left[\rule{0pt}{10pt}16t+3t^3\right]_0^{2\pi}=160\pi+120\pi^3 \end{aligned}\]
We look at applications starting on the next page.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum